EXAMEN DE COMIPEMS.
La actividad es:
Entregar en hojas blancas todos los ejercicios de las actividades que aparecen aquí.
Debe tener carátula, se debe anotar el tema y en seguida los ejercicios resueltos (SÓLO LOS EJERCICIOS).
Si algún tema o temas no tienen explicación, es porque se relacionan con otros, sólo analicenlo.
1. significado y uso de numeros.
Numeros enteros.
1.1 significado y uso de las operaciones basicas con numeros enteros.
1.2 resolucion de problemas con operaciones básicas.
Adición.
Significa que se agregarán números tiene que ser negativo con negativo o positivo con positivo. Si ambos números son positivos el resultado tendrá signo positivo, si ambos números son negativos el resultado tendrá signo negativo. Por ejemplo.
3+6=9 en este ejemplo el 3 es positivo y el 6 es positivo por lo tanto el resultado es 9 positivo.
-7-14= -21 en este ejemplo el 7 es negativo y el 14 es negativo por lo tanto el resultado es 21 negativo.
Sustracción.
Cuando tenemos un número positivo y un número negativo debemos hacer una sustracción es decir al número más grande le quitaré la cantidad que indica el número más pequeño el resultado tendrá el signo del número más grande.
Ejemplo.
100-45=55 en este ejemplo el 100 es más grande que el 45 negativo por lo tanto al realizar mi sustracción el resultado será 55 y el signo que debe tener es positivo ya que el número más grande es el 100 y tiene signo positivo.
-80+30= -50 en este ejemplo el 80 es negativo y es el número más grande, por lo tanto a 80 le quitaré 30 el resultado será 50 pero el signo será negativo ya que el 80 es el más grande y el signo que tiene es negativo.
Multiplicación con números positivos y negativos.
Explicación.
Un número positivo se representa con el signo más o sin el signo. Puede ser 5 o también +5, en ambos casos es 5 positivo.
Un número negativo se representa con un guión a media altura. Así: -8, en este caso este número es 8 negativo.
Cuándo se multiplica.
Para identificar cuándo se debe realizar una multiplicación, los signos que se utilizan son la x, un punto a la mitad de los números o paréntesis rodeando a los números. Así:
5x7=35
8•9=72
(7)(4)=28
5(8)=40
Ley de signos para multiplicación.
Cuando multiplico dos números con signos iguales el resultado es positivo. Ejemplo.
(-4)(-5)=20
si multiplico números negativos el resultado es positivo
(7)(3)=21
si multiplico números positivos el resultado es positivo
Cuando multiplicó números con signos diferentes el resultado es negativo. Ejemplo.
(7)(-2)= -14
(-9)(4)= -36
División con positivos y negativos.
Se presentan cuatro casos:
1. dividendo y divisor son positivos. Resultado positivo
2. dividendo y divisor son negativos. Resultado positivo.
10÷5=2
-20÷-4=5
3. dividendo negativo y divisor positivo. Resultado negativo.
4. dividendo positivo y divisor negativo. Resultado negativo.
-15÷3=-5
16÷-8=-2
Actividad. Resuelve las siguientes operaciones, respetando las indicaciones previas.
10+8=
-4-6=
8+6=
-7-3=
4+4=
-7-4=
9+3=
-12-2=
-10-5=
4+2=
8+5=
7-2=
-4+2=
8-2=
-6+4=
9-2=
-8+6=
10-2=
-10+8=
(3)(2)=
(-4)(-2)=
(5)(4)=
(-4)(3)=
(2)(-1)=
(4)(-4)=
-20:4=
10:2=
-8:2=
60:6=
-10:5=
Numero fraccionarios y decimales.
1.3 relaciones de proporcionalidad.
Tema. Proporcionalidad directa.
La proporcionalidad es una relación que existe entre dos cantidades.
En el caso de la proporcionalidad directa la relación es que: si la primer cantidad aumenta la segunda también lo hace.
Ejemplo.
Luis comprará pintura, cada litro tiene un precio de 75 pesos si necesita 15 litros ¿Cuál será el costo total?
Para calcular cualquier situación de proporcionalidad directa se tiene que utilizar una regla de tres.
Se multiplican las cantidades cruzadas y el resultado se divide entre la tercer cantidad.
Actividad. Calcula la proporcionalidad directa de las siguientes situaciones.
Carlos compró un par de tenis, que cuestan $280, ¿cuál sería el costo si compra 2, 4, 8, 10?
María compró una chamarra que costaba $340, ¿cuánto tendría que pagar si comprará 2, 6, 10 y 12 chamarras?
Pedro compró donas que costaban $15 cada una, si compró 6, 15, 20 y 25 ¿cuánto pagó?
Juan compró una bolsa que cuesta $120, ¿cuál sería el costo si comprará 2, 5, 10 y 15 bolsas?
María compró una chamarra que costaba $340, ¿cuánto tendría que pagar si comprará 2, 6, 10 y 12 chamarras?
Pedro compró donas que costaban $15 cada una, si compró 6, 15, 20 y 25 ¿cuánto pagó?
Juan compró una bolsa que cuesta $120, ¿cuál sería el costo si comprará 2, 5, 10 y 15 bolsas?
Tema. Proporcionalidad inversa.
La proporcionalidad es la relación que existe entre dos cantidades.
La proporcionalidad inversa indica que si una cantidad aumenta la otra disminuye o si una cantidad disminuye la otra aumenta.
Ejemplo.
José y un compañero pintan una casa en 12 días, si invitaran a otras dos personas a trabajar ¿Cuántos días tardarían en pintar la casa?
Paso 1.
Se ordenan los datos.
Paso 2.
Se realiza un despeje, esto significa que el dato que está solo quedará como divisor.
Paso 3.
Se realiza la multiplicación y la división correspondientes. El resultado será el dato que hace falta.
Nota. Sin importar que dato haga falta siempre se realiza este proceso.
La proporcionalidad es la relación que existe entre dos cantidades.
La proporcionalidad inversa indica que si una cantidad aumenta la otra disminuye o si una cantidad disminuye la otra aumenta.
Ejemplo.
José y un compañero pintan una casa en 12 días, si invitaran a otras dos personas a trabajar ¿Cuántos días tardarían en pintar la casa?
Paso 1.
Se ordenan los datos.
Paso 2.
Se realiza un despeje, esto significa que el dato que está solo quedará como divisor.
Paso 3.
Se realiza la multiplicación y la división correspondientes. El resultado será el dato que hace falta.
Nota. Sin importar que dato haga falta siempre se realiza este proceso.
Actividad. Resuelve los siguientes problemas aplicando la proporcionalidad inversa.
En un establo 12 caballos consumen una carga de alimento en 9 días. Si llegan seis caballos más ¿En cuántos días se comerían la misma cantidad de alimento?
Un grupo de personas contrató un autobús a un precio fijo para un viaje, al principio viajarían 44 personas y el precio para cada uno sería de 9 peso, pero finalmente viajaron 36 ¿cuánto tendría que pagar cada uno?
Un coche que circula a 70 kilómetros por hora tarda 9 horas en cubrir una distancia entre dos ciudades, si vuelve a realizar el mismo viaje pero tarda 5 horas ¿A qué velocidad circulaba en el segundo viaje?
4 llaves de agua llenar un depósito en 10 horas. Si usáramos 8 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
Dos llaves llenan un depósito en 5 horas, si se usarán 10 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
En un establo 12 caballos consumen una carga de alimento en 9 días. Si llegan seis caballos más ¿En cuántos días se comerían la misma cantidad de alimento?
Un grupo de personas contrató un autobús a un precio fijo para un viaje, al principio viajarían 44 personas y el precio para cada uno sería de 9 peso, pero finalmente viajaron 36 ¿cuánto tendría que pagar cada uno?
Un coche que circula a 70 kilómetros por hora tarda 9 horas en cubrir una distancia entre dos ciudades, si vuelve a realizar el mismo viaje pero tarda 5 horas ¿A qué velocidad circulaba en el segundo viaje?
4 llaves de agua llenar un depósito en 10 horas. Si usáramos 8 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
Dos llaves llenan un depósito en 5 horas, si se usarán 10 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
1.4 significado y uso delas operaciones basicas con numeros fraccionarios y decimales.
Tema. Tipos de fracciones.
Una fracción es la parte de un entero y se compone de los siguientes elementos:
Los tipos de fracciones son:
Fracción propia el numerador es menor que el denominador.
1/4, 2/6, 3/9
Fracción impropia el numerador Es mayor que el denominador.
6/4, 9/5, 8/3
Fracción mixta está formada por una parte entera y una fracción.
4 3/4, 6 1/5
Fracción entera tanto numerador como denominador tienen la misma cantidad
2/2, 4/4, 7/7
Tema. Suma de fracciones.
Los pasos son:
- El primer numerador se multiplica por el segundo denominador.
- El primer denominador se multiplica por el segundo numerador.
- Se multiplican los denominadores, el resultado es el nuevo denominador.
- Los resultados de las multiplicaciones cruzadas se suman y se obtiene el nuevo numerador.
- En caso de que la nueva fracción se puede simplificar, se realiza.
Ejemplo.
Se multiplica 2 por 8 y se anota arriba después de multiplicar 3 por 4 y se anota arriba esos dos números se van a sumar y será el nuevo numerador.
Se multiplica 3 por 8 y será el nuevo denominador.
En este caso la fracción se puede simplificar hasta 7/6.
Tema. Resta de fracciones.
Los pasos son:
- El primer numerador se multiplica por el segundo denominador.
- El primer denominador se multiplica por el segundo numerador.
- Se multiplican los denominadores, el resultado es el nuevo denominador.
- Los resultados de las multiplicaciones cruzadas se restan y se obtiene el nuevo numerador.
- En caso de que la nueva fracción se puede simplificar, se realiza.
Ejemplo.
Se multiplica 9 por 5 y se anota arriba, se multiplica 11 por 1 y se anota arriba, estos números se restan y resulta en el nuevo numerador.
Se multiplica 11 por 5 y el resultado es el nuevo denominador.
En este caso la fracción no se puede reducir y queda así.
Tema. Multiplicación de fracciones.
1. Se multiplican los numeradores y el resultado es el nuevo numerador
2. Se multiplican los denominadores y el resultado es el nuevo denominador.
3. En caso de que se puede simplificar, se realiza.
Ejemplo.
Tema. División de fracciones.
1. Se multiplica el primer numerador por el segundo denominador, el resultado queda como el nuevo numerador.
2. Se multiplica el primer denominador por el segundo numerador el resultado queda como el nuevo denominador.
3. Se simplifica, en caso de que sea posible.
Ejemplo.
Tema. Conversión de fracción mixta a impropia.
Los pasos son:
1. Se multiplica el denominador por la parte entera y se suma la cantidad indicada en el numerador el resultado será el nuevo numerador de la fracción impropia.
2. El nuevo denominador será la misma cantidad que tenía la fracción mixta.
Ejemplo.
Tema. Conversión de fracción impropia a mixta.
Los pasos son:
1. El numerador queda como dividendo y el denominador queda como divisor.
2. El cociente será la parte entera el residuo será el nuevo numerador si el divisor se repetirá como denominador.
Tema. Conversión de fracción a decimal.
Para convertir una fracción a decimal se realiza lo siguiente:
1. El numerador queda como dividendo.
2. El denominador queda como divisor.
3. Se realiza la división correspondiente, el resultado es el número decimal equivalente a la fracción.
4. Si hay enteros solo se suman al final.
Ejemplo.
Para convertir un número decimal a fracción, se realiza lo siguiente:
1. El número decimal queda como numerador, se debe quitar el punto.
2. El denominador será el número 1 y se agregarán seros dependiendo de la cantidad de cifras que haya en él numerador.
3. Si se puede simplificar, se realiza.
Ejemplos.
Tema. Multuplicación con decimal y fracción.
Para resolver este tipo de operaciones se debe convertir alguno de ellos para tener sólo fracciones o decimales.
Posteriormente se aplican los pasos previamente explicados para operaciones con fracciones y operaciones con decimales.
Tema. División con decimal y fracción.
Para resolver este tipo de operaciones se debe convertir alguno de ellos para tener sólo fracciones o decimales.
Posteriormente se aplican los pasos previamente explicados para operaciones con fracciones y operaciones con decimales.
Tema. Suma de fracciones con mínimo común múltiplo.
Pasó 1. Se obtiene el mínimo común múltiplo qué será el nuevo denominador.
Paso 2. El mínimo común múltiplo se dividirá entre el primer denominador y el resultado se multiplicará por el primer numerador, después el mínimo común múltiplo se dividirá entre el segundo denominador y se multiplicará por el segundo numerador posteriormente este proceso se repetirá para todas las fracciones.
Paso 3. Los nuevos numeradores eres soltera en el numerador final por último se recorre el nuevo denominador Qué es el mínimo común múltiplo.
Ejemplo.
Actividad. Resuelve las siguientes sumas y restas de fracciones.
7/24+5/6=
2/3+4/9=
5/15+9/20=
35/40+4/5=
6/9+3/16=
21/35+3/18=
12/20+9/35=
5/6-2/3=
5/4-1/6=
2/3-1/4=
5/6-3/4=
7/9-1/6=
4/5-1/7=
3/4-1/5=
7/24+5/6=
2/3+4/9=
5/15+9/20=
35/40+4/5=
6/9+3/16=
21/35+3/18=
12/20+9/35=
5/6-2/3=
5/4-1/6=
2/3-1/4=
5/6-3/4=
7/9-1/6=
4/5-1/7=
3/4-1/5=
Actividad. Resuelve las siguientes divisiones de fracciones.
6/9:3/5=
4/5:3/9=
5/4:3/8=
9/4:8/5=
6/4:9/10=
6/8:2/3=
4/5:3/9=
5/4:3/8=
9/4:8/5=
6/4:9/10=
6/8:2/3=
Actividad. Resuelve las siguientes multiplicaciones de fracciones.
5/6-2/3=
5/4*1/6=
2/3*1/4=
5/6*3/4=
7/9*1/6=
4/5*1/7=
5/6-2/3=
5/4*1/6=
2/3*1/4=
5/6*3/4=
7/9*1/6=
4/5*1/7=
1.5 porcentajes.
Tema. Frecuencia absoluta y frecuencia relativa.
La frecuencia absoluta se refiere a la cantidad de veces que se repite un dato.
Ejemplo.
Se tomó la temperatura en un poblado durante 15 días los resultados fueron los siguientes:
16°, 15°, 15°, 14°, 12°, 16°, 12°, 14°, 16°, 8°, 5°, 3°, 12°, 15°, 16°.
¿ Cuál es la frecuencia absoluta de los datos anteriores?
Primero se deben ordenar los datos de menor a mayor. Posteriormente se anota la frecuencia absoluta para cada dato y se suman para obtener el total de resultados.
Tema. Frecuencia relativa.
La frecuencia relativa es el resultado de dividir la frecuencia absoluta entre el total de resultados.
Ejemplo.
Dividir 1÷15= .066
Por último, los resultados de frecuencia relativa se pueden convertir a porcentaje, lo más sencillo mover el punto decimal dos espacios hacia la derecha esa cantidad es la que corresponde al porcentaje.
La frecuencia relativa es el resultado de dividir la frecuencia absoluta entre el total de resultados.
Ejemplo.
Dividir 1÷15= .066
Por último, los resultados de frecuencia relativa se pueden convertir a porcentaje, lo más sencillo mover el punto decimal dos espacios hacia la derecha esa cantidad es la que corresponde al porcentaje.
Tema. Cálculo de probabilidad en porcentaje.
Al tener la probabilidad en decimal lo único que se debe realizar es convertirlo a porcentaje, para ello se debe considerar la siguiente tabla.
Al tener la probabilidad en decimal lo único que se debe realizar es convertirlo a porcentaje, para ello se debe considerar la siguiente tabla.
Ejemplo.
Juan colocó en un recipiente canicas de diferentes colores cuál sería la probabilidad en fracción, en decimal y en porcentaje para cada color.
Los pasos para calcular el porcentaje de una cantidad son:
1. Se nota la cantidad de la que se obtendrá el porcentaje.
2. A manera de fracción se anota el número 100 abajo de la cantidad total ( ya que la cantidad total corresponde al 100%).
3. Se anota el porcentaje que se desea buscar, cuidando que los datos estén bien ordenados.
4. Se aplica una regla de tres para obtener el resultado.
Ejemplo.
Calcular el 20% de 50
sabiendo que 50 equivale al cien por ciento, se multiplica 20 por 50 y el resultado se divide entre 100.
20x50 = resultado 10.
100
eso indica que el 20% de 50 es igual a 10.
Actividad. Calcula el porcentaje para cada una de las cantidades.
12% de 250
30% de 500
36% de 1000
56% de 28
25% de 50
32% de 400
15% de 30
20% de 540
1.6 potenciacion y radicacion.
Raíz cuadrada.
Para calcular la raíz cuadrada de un número se realiza lo siguiente:
- Se separan de derecha a izquierda los números colocando una comer cada dos cifras.
- Después de separarlos se buscará un número que multiplicado por sí mismo de forma exacta o aproximada en el primer número de la izquierda, este número que se multiplica por sí mismo se anota en el primer renglón y el sobrante cenote de bajo del primer número de la izquierda.
- Enseguida se baja el siguiente par de números quedando entonces una nueva cifra creada por que residuo del primer número de la izquierda con los números que se bajaron.
- El número que se anotó en el primer renglón se duplicará y se anotará en el segundo renglón, este número se usará para una multiplicación aplicando la "regla de la L" que servirá para encontrar el nuevo número que se formó. Como regla el número que se anota en la multiplicación debe ser el mismo número abajo que arriba por ejemplo 41 por 1, 42 por 2, 43 por 3, 44 por 4, etc.
- A partir de aquí se repetirán todos los pasos anteriores.
El resultado de la raíz será el número que se forma en el primer renglón, para comprobarlo se multiplica este número por sí mismo y en casa de que no sea exacto al número buscado se le debe sumar el residuo de la raíz, observa el ejemplo.
Ejemplo.
Tema. Raíz cuadrada (resultado en decimales).
1 Se separan grupos de dos cifras a partir de la coma hacia la izquierda (la parte entera) y hacia la derecha (la parte decimal).
2 Si el radicando tiene en su parte decimal un número impar de cifras, se añade un cero a la derecha.
3 Prescindiendo de la coma, se extrae la raíz cuadrada del número que resulta.
4 En la raíz, a partir de la derecha, colocamos un número de cifras decimales igual al número de pares de cifras decimales que hubiere en el radicando. En el resto y también a partir de la derecha, se separan tantas cifras decimales como haya en el radicando.
Ejercicios de raíz cuadrada con decimales
Calcular la raíz cuadrada de:


Resolver la raíz cuadrada de:


√315
√518
√758
√985
1.7 resolucion de problemas con numeros fraccionarios o decimales.
2 algebra.
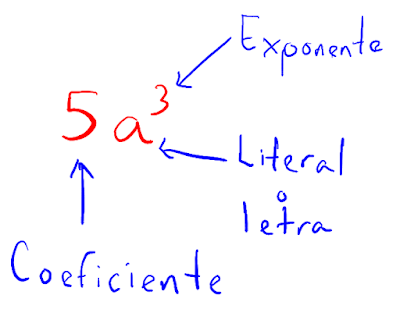
2.1 significado y uso de las literales
Expresion algebraicas.
2.2 expresion comun de problemas algebraicos de adicion y sustraccion.
2.3 resolucion de problemas con expresiones algebraicas.
Tema. Operaciones con monomios.
Un monomio es un término algebraico compuesto por:
Adición con monomios.
Se debe considerar lo siguiente:
1. Los signos en los coeficientes deben ser iguales para que se realice la adición.
2. Las letras y los exponentes deben ser los mismos.
3. Si alguna parte del monomio es diferente de la que se intenta agregar no se puede realizar y el resultado serán los mismos términos.
Ejemplo.
3a²+5a²=8a²
-3c³-4c³=-7c³
4a²+5a³=4a²+5a³
Sustracción con monomios.
Se debe considerar lo siguiente:
1. Los signos en los coeficientes deben ser diferentes para que se realice la sustracción.
2. Las letras y los exponentes deben ser los mismos.
3. Si alguna parte del monomio es diferente de la que se intenta sustraer no se puede realizar y el resultado serán los mismos términos.
Ejemplo.
-3a²+5a²=3a²
3c³-4c³=-1c³
-4a²+5a³=-4a²+5a³
Multiplicación de monomios.
Se debe considerar lo siguiente:
1. Los coeficientes se multiplicarán respetando la ley de signos.
2. Si en los términos multiplicados hay letras que son iguales, se anotarán las letras y se sumarán los exponentes.
3. En caso de que haya letras que están solas, estás simplemente se anotarán ya que no tienen con quién sumarse.
4. En el resultado las letras se pueden anotar alfabéticamente o se anota primero la letra con mayor exponente a la menor.
Ejemplo.
(-4g²)(5g²)= -20g⁴
(-3c²)(-2a³)= 6a³c²
División de monomios.
Se debe considerar lo siguiente:
1. Se dividen los coeficientes respetando la ley de signos.
2. Si hay letras iguales se restan sus exponentes, al primer exponente se le restará el segundo.
3. En caso de que haya letras que están solas, estás simplemente se anotarán ya que no tienen con quién restarse.
4. En el resultado las letras se pueden anotar alfabéticamente o se anota primero la letra con mayor exponente a la menor.
(-10f⁴)÷(2f²)= -5f²
(-20s³)÷(-5s²)= 4s
Actividad. Resuelve las siguientes operaciones con monomios atendiendo las indicaciones de la explicación.
10b^2-5b^2=
-20c^4+17c^4=
9b^3-5b^3=
25b^4-5b^4=
50b^7-10b^7=
5a^6*-7a^4=
6b^7*8b^3=
-17z^4*8z^4=
1y^2*2y^3=
6g^4*-5g^2=
3a^2/3a^6=
40b^5/4b^6=
18000b^2/1b^1=
900c^3/2c^2=
30c^2/15c^1=
Ecuaciones de primer grado.
2.4 resolucion de ecuaciones de primer grado.
2.5 resolucion de problemas con ecuaciones de primer.
Tema. Ecuaciones de primer grado. Forma x+a=b
Una ecuación es una operación en la que debemos calcular el valor de un número desconocido.
Debemos considerar lo siguiente:
x es el valor desconocido
a representa un número
b representa un número
Los pasos para resolver una ecuación de esta forma son:
ECUACIÓN ORIGINAL.
x+24=55
pasó 1 Se acomodan los términos, del lado izquierdo del signo igual se anota la x, del lado derecho del signo igual se anotan los números. Considerando que el número qué cambia de posición también cambiará de signó.
x=55-24 sólo cambió el 24 positivo a negativo, el 55 no cambia de signo porque no lo movimos
pasó 2 se resuelve la operación
x=31
pasó 3 el resultado se utiliza para realizar la comprobación
31+24=55 el resultado que en este caso es 31 se nota en lugar de la letra x, ahora se resuelve la operación y se comprueba qué 31 es el valor correcto.
Tema. Ecuaciones en la forma ax=b
Los pasos para resolver este tipo de ecuación son:
1. Se acomodan los términos, del lado izquierdo el signo igual está la letra x, del lado derecho del signo igual se anota el número que acompañaba a la letra x y será el divisor.
2. Se resuelve la división correspondiente cuidando que el resultado tenga el signo correcto.
3. El valor desconocido será el resultado de la división y se usará para hacer la comprobación.
Ejemplo.
6x=48 ecuación original
x= 48÷6 se acomodan los números
x= 8 este es el resultado y se usará para la comprobación
COMPROBACIÓN.
6(8)=48 el valor desconocido se anota en el lugar de la letra x y se usará para multiplicarlo.
48=48 el resultado es correcto
Tema. Ecuaciones de primer grado. Forma ax+b=c
Una ecuación es una operación en la que debemos calcular el valor de un número desconocido.
Debemos considerar lo siguiente:
x es el valor desconocido
a representa un número
b representa un número
c representa un número
Los pasos para resolver una ecuación de esta forma son:
ECUACIÓN ORIGINAL.
1. los términos que tienen x se anotan del lado izquierdo del signo igual, considerando qué cambia que el término que se mueve cambia a su operación contraria.
2. los términos que no tienen x se anotan de lado derecho del signo igual, considerando qué el término que se mueve cambia a su operación contraria.
3. se resuelven las operaciones correspondientes cuidando los signos
4. el número que acompaña a la letra x, se mueve al otro lado para hacer la división.
5. el resultado se utiliza para hacer la comprobación.
Ejemplo.
-11x+12
|
=
| 144 |
-11x
|
=
| 144-12 |
-11x
|
=
| 132 |
x
|
=
| 132/-11 |
x
|
=
| -12 |
Comprobación
|
-11(-12)+12
|
=
| 144 |
132+12
|
=
| 144 |
144
|
=
| 144 |
Ejemplo.
-8x-15
|
=
| -111 |
-8x
|
=
| -111+15 |
-8x
|
=
| -96 |
x
|
=
| -96/-8 |
x
|
=
| 12 |
Comprobación
|
-8(12)-15
|
=
| -111 |
-96-15
|
=
| -111 |
-111
|
=
| -111 |
Tema. Ecuación forma ax+b=cx+d
los pasos para resolver esta ecuación son:
1. los términos que tienen x se anotan del lado izquierdo del signo igual, considerando qué cambia que el término que se mueve cambia a su operación contraria.
2. los términos que no tienen x se anotan de lado derecho del signo igual, considerando qué el término que se mueve cambia a su operación contraria.
3. se resuelven las operaciones correspondientes cuidando los signos
4. el número que acompaña a la letra x, se mueve al otro lado para hacer la comprobación.
5. el resultado se utiliza para hacer la comprobación.
Ejemplo.
-6x-10
|
=
| 4x+80 |
-6x-4x
|
=
| 80+10 |
-10x
|
=
| 90 |
x
|
=
| 90/-10 |
x
|
=
| -9 |
Comprobación
|
-6(-9)-10
|
=
| 4(-9)+80 |
54-10
|
=
| -36+80 |
44
|
=
| 44 |
Ejemplo.
7x+10
|
=
| -7x+94 |
7x+7x
|
=
| 94-10 |
14x
|
=
| 84 |
x
|
=
| 84/14 |
x
|
=
| 6 |
Comprobación
|
7(6)+10
|
=
| -7(6)+94 |
42+10
|
=
| -42+94 |
52
|
=
| 52 |
Actividad. Obtener el valor de X para las siguientes ecuaciones y realiza su comprobación.
13x+8
|
=
| -14x-343 |
12x+1
|
=
| -15x-404 |
-5x+9
|
=
| 12x+179 |
-x+15
|
=
| 5x+15 |
-6x-10
|
=
| 4x+80 |
Sistema de ecuaciones lineales de dos ecuaciones con dos incognitas.
2.6 resolucion de sistemas lineales de dos ecuaciones con dos incognitas.
2.7 resolucion de problemas con sistemas de dos ecuaciones lineales con dos incognitas.
Tema. Sistema de ecuaciones.
Método de sustitución
1 Se despeja una incógnita en una de las ecuaciones.
2 Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita.
3 Se resuelve la ecuación.
4 El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.
5 Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo

1 Despejamos una de las incógnitas en una de las dos ecuaciones. Elegimos la incógnita que tenga el coeficiente más bajo.

2 Sustituimos en la otra ecuación la variable x, por el valor anterior:

3 Resolvemos la ecuación obtenida:

4 Sustituimos el valor obtenido en la variable despejada.

5 Solución

1x+3y=6
5x-2y=13
Tema. Sistema de ecuaciones método de igualación.
Sistema.
7x+4y=13
5x-2y=19
1. despejamos cualquiera de las incógnitas, por ejemplo, si despejamos x tiene que ser en ambas ecuaciones.
2. Ahora se igualan las ecuaciones que se despejaron.
3. Después de igualarlas se intercambian de lado los números que están dividiendo para quedar multiplicando, posteriormente se resuelven las operaciones hasta llegar al valor de y.
4. Al tener el valor de y, se sustituye en cualquiera de las ecuaciones para calcular el valor de x.
5. Por último se realizan la comprobación sustituyendo los valores encontrados en cualquier ecuación.
Actividad. Resuelve los siguientes sistemas de por el método de igualación.
1x+6y=27
7x-3y=9
3x-2y=-2
5x+8y=-60
Tema. Sistema de ecuaciones por método de suma o resta.
Método de suma o resta
1 Se preparan las dos ecuaciones, multiplicándolas por los números que convenga.
2 La restamos, y desaparece una de las incógnitas.
3 Se resuelve la ecuación resultante.
4 El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve.
5 Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo

Lo más fácil es suprimir la y, de este modo no tendríamos que preparar las ecuaciones; pero vamos a optar por suprimir la x, para que veamos mejor el proceso.

Restamos y resolvemos la ecuación:

Sustituimos el valor de y en la segunda ecuación inicial.

Solución:

6x-5y=-9
4x+3y=13
7x-15y=1
-1x-6y=8
Ecuaciones de segundo grado.
2.8 productos notables y factorizacion.
Tema. Resolución de ecuación de segundo grado por factorización.
Los pasos para resolver una ecuación de segundo grado por factorización son:
1. Ordenar la ecuación indicada a la forma ax²+bx+c=0
2. Identificar los factores que al multiplicarse resultan en la ecuación de segundo grado ordenada, para ello se puede hacer la siguiente consideración, en los factores debe existir dos números que multiplicados resulten en el valor de c y sumados o restados resulten en el valor de b.
3. Multiplicar los factores y comprobar que el resultado sea la ecuación de segundo grado ordenada.
4. Los valores de x1 y x2 se obtendrán al cambiar el signo de los factores al contrario.
Ejemplo.
Resuelve la ecuación:
x²= -5x +24
Paso 1. Ordenar la ecuación.
x² +5x -24=0
Paso 2. Identificar los factores que al multiplicarse resulten en la ecuación ordenada.
(x+8) ( x-3)
Paso 3. Verificar que los factores resulten en la ecuación ordenada.
Paso 4. Los valores de x1 y x2 se obtendrán al cambiar el signo de los factores al contrario.
Actividad. Resuelve las siguientes ecuaciones aplicando la factorización.
x²-x-6=0
x²+7x=18
2.9 resolucion de ecuaciones de segundo grado.
Tema. Ecuación de segundo grado.
Se llama ecuación de segundo grado Por qué es exponente más alto es 2.
La fórmula que se utiliza para resolver este tipo de ecuación es:
Como en cualquier fórmula cada letra tiene un valor para identificarlo se considera lo siguiente:
- El valor de la letra a corresponde al número que acompaña a la x².
- El valor de la letra b corresponde al número que acompaña a la x sinexponente.
- El valor de la letra c corresponde al número que no tiene x.
1. Identificar cuánto vale a, b, c.
2. Sustituir las letras por los valores identificados cuidando que el signo sea el correcto.
Si se ordena de forma correcta lo único que queda hacer es resolver las operaciones.
3. Al llegar a este paso se separa la operación, por una se utilizará el signo positivo y por otra el signo negativo, teniendo entonces 2 resultados.
4. Se realizará la comprobación para ello utilizaremos el resultado que sea más fácil de manejar que en este caso es 2.
Sólo se debe anotar el número 2 dentro de un paréntesis en lugar de las letras x
5. Al llegar a la igualdad 0 nuestros resultados y procedimientos son correctos.
3x²-5x+2=0
4x²+3x-22=0
2.10 relaciones de proporcionalidad directa.
2.11 relaciones de proporcionalidad en el plano cartesiano.
Tema. Función cuadrática. (Proporcionalidad, gráficas).
A partir de una situación de proporcionalidad se pueden registrar los datos y graficarlos.
Ejemplo.
Mario entró a trabajar y cada quincena ahorrará 250 pesos si desea comprar un televisor. ¿cuánto tiempo tarda en juntar 3000 pesos?
Actividad. Analiza los siguientes problemas, elabora la tabla y gráficas correspondientes.
1. En una casa se da gasto de 1000 semanales, y se requiere saber en cuánto tiempo da dará se dará gasto acumulado de 15000 pesos.
2. Jorge trabaja en una tienda y cada semana le pagan 500 pesos, cuánto se tardará en juntar 3000.
3. Cuál es el tiempo que tardará en llenarse un recipiente de 10500 ml si se abre una llave de agua y por cada minuto vierte 275ml.
3 manejo de la informacion estadistica.
3.1 analisis de la informacion estadistica: indices.
3.2 graficas de barras y circulares.
3.3 tablas de frecuecia absoluta y relativa.
Tema. Frecuencia absoluta y frecuencia relativa.
La frecuencia absoluta se refiere a la cantidad de veces que se repite un dato.
Ejemplo.
Se tomó la temperatura en un poblado durante 15 días los resultados fueron los siguientes:
16°, 15°, 15°, 14°, 12°, 16°, 12°, 14°, 16°, 8°, 5°, 3°, 12°, 15°, 16°.
¿ Cuál es la frecuencia absoluta de los datos anteriores?
Primero se deben ordenar los datos de menor a mayor. Posteriormente se anota la frecuencia absoluta para cada dato y se suman para obtener el total de resultados.
Tema. Frecuencia relativa.
La frecuencia relativa es el resultado de dividir la frecuencia absoluta entre el total de resultados.
Ejemplo.
Dividir 1÷15= .066
Por último, los resultados de frecuencia relativa se pueden convertir a porcentaje, lo más sencillo mover el punto decimal dos espacios hacia la derecha esa cantidad es la que corresponde al porcentaje.
La frecuencia relativa es el resultado de dividir la frecuencia absoluta entre el total de resultados.
Ejemplo.
Dividir 1÷15= .066
Por último, los resultados de frecuencia relativa se pueden convertir a porcentaje, lo más sencillo mover el punto decimal dos espacios hacia la derecha esa cantidad es la que corresponde al porcentaje.
Actividad. Calcula la frecuencia absoluta, la frecuencia relativa y el porcentaje para cada una de las siguientes situaciones.
El total de chocolates vendidos por una tienda fue de 140 con pasas, 230 con galleta, 270 blanco, 145 con almendras y 178 chocolate dulce.
Francisco tiene un puesto de revistas el lunes vendió 22, martes 15, miércoles 8, jueves 20 viernes 10.
Francisco tiene un puesto de revistas el lunes vendió 22, martes 15, miércoles 8, jueves 20 viernes 10.
3.4 medidas de tendencia central
Tema. Análisis de datos.
En un grupo de datos se pueden analizar los siguientes elementos:
1. Moda: la moda se refiere a los datos que aparecen con mayor frecuencia, si hay 2 modas se llama bimodal, si hay más de dos será multimodal.
2, 3, 3, 4, 4, 4, 5, 5
Moda= 4.
2. Mediana: es el número que se encuentra a la mitad de un grupo de datos, después de que han sido ordenados de menor a mayor o viceversa.
2, 3, 4, 4, 5, 5, 5, 6, 6.
Mediana=5
Si la cantidad de datos es par la mediana será el promedio de las dos cantidades.
7, 8, 9, 10, 11, 12
9+10=19. 19÷2=9.5
Mediana= 9.5
3. Media o promedio: es el número obtenido a partir de la suma de todos los datos, dividida entre la cantidad de datos.
14, 54, 25, 32, 47, 28
Suma 200÷6=33.3
Media o promedio = 33.3
Actividad. analiza la siguiente situación y obtén la moda, la media y la mediana.
Carlos prepara una presentación con los datos que obtuvo de su empresa, las ganancias de cada mes
enero 25000, febrero 16000, marzo 18 mil, abril 19000, mayo 25000, junio 27 mil, julio 15000, agosto 13 mil, septiembre 14000, octubre 12 mil, noviembre 13000, diciembre 25000.
Tema. Media ponderada.
La media ponderada se obtiene al otorgar un valor a cada uno de los datos de un grupo de datos.
Para ello se multiplica cada dato por el valor asignado y se dividirá entre la suma de todos los valores. El resultado será la media ponderada.
La calificación final de una asignatura es un ejemplo de una media ponderada ya que cada una de las variables tiene un valor.
En el siguiente ejemplo el examen inicial tiene un valor de 3, el trabajo escrito 1, el trabajo final 2 y el examen final 4.

Se multiplica la calificación de cada una de las variables por el valor qué se le asignó, todos estos resultados se suman y se dividen entre la cantidad de valores que se otorgaron.

La nota final del alumno en esta asignatura es de 6,14. como la nota es muy próxima a las notas sacadas en los exámenes. Esto es a causa de que los exámenes eran más importantes y tenían unos pesos mucho mayores que los de los trabajos.
3.5 nociones de probabilidad y muestreo
Tema. Frecuencia absoluta y frecuencia relativa.
Ya está anotado, se repite.
4 formas geometricas
4.1 rectas y angulos
Tema. Ángulos formados en líneas paralelas atravesadas por una transversal.
Las zonas en donde se ubican los ángulos son interna que es dentro de las paralelas y externa que es por fuera de las paralelas.
Los tipos de ángulos que se forman son:
Ángulos colaterales internos: están dentro de las paralelas y del mismo lado de la transversal.
Ángulos colaterales externos: están fuera de las paralelas y del mismo lado de la transversal.
Ángulos alternos internos: están dentro de las paralelas y en lados opuestos de la transversal.
Ángulos alternos externos: están dentro de las paralelas y en lados opuestos de la transversal.
Ángulos Opuestos por el vértice: como el nombre lo indica están en lados contrarios en relación al vértice.
Ángulos correspondientes: son parejas de ángulos que tienen las mismas medidas porque están ubicados en la misma posición uno en relación a otro.
Se puede calcular la medida de todos los ángulos a partir de un solo ángulo indicado. Observa el ejemplo.
Sabiendo que un círculo mide 360 grados, la mitad serían 180 grados, por lo tanto al indicar un ángulo de 40 grados en el ángulo número 2, el ángulo número uno tendría una medida de 140 grados.
Si se suman los grados entre los ángulos 1 y 2, resulta en 180 grados.
Por consecuencia las medidas de los ángulos 3 4 5 6 y 7 se obtendrán a partir de los ángulos 1 y 2, ya que al aplicar la correspondencia de ángulos se repite la medida.
4.2 figuras planas
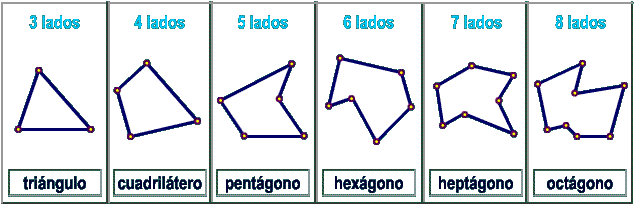
Tema. Partes de un polígono.
Vértice. Es el punto donde se unen dos líneas rectas.
Arista. Es cada una de las líneas rectas de una figura, también conocidas como lado.
Ángulo. Es la medida de separación en grados entre dos aristas.
¿Es un polígono?
Los polígonos son formas bidimensionales. Están hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).
 |  |  |
| Polígono (lados rectos) | No es un polígono (tiene una curva) | No es un polígono (abierto, no cerrado) |
Tema. Polígonos simples y complejos.
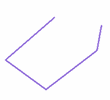
Un polígono simple es aquél en donde ninguno de sus lados se cruza o encima con otro.

Ejemplo de polígono simple, ningún lado se cruza.
Un polígono complejo es aquél en el que por lo menos uno de sus lados o aristas se cruza encima con otra u otras
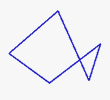
Ejemplo de polígono complejo, uno de sus lados o aristas se cruza con otro.
Tema. Polígono regular e irregular.
Polígono regular. Es aquella figura en la que todos sus lados o aristas miden lo mismo y también sus ángulos miden lo mismo.

Polígono irregular. Es aquella figura en la que por lo menos uno de sus lados o aristas es diferente al de los otros, de la misma forma por lo menos uno de sus ángulos tiene diferente medida a los otros.
Nota. Para que se considere un polígono debe estar formado por líneas rectas si alguna línea es curva deja de ser polígono. También todas las líneas deben estar unidas si hay una separación deja de ser polígono.
Tema. Creación de polígonos a partir de su ángulo central.
Los pasos para crear un polígono desde su ángulo central son:
Observa las imagenes.
Los pasos para crear un polígono desde su ángulo central son:
- Se marca un punto que servirá de centro en nuestra figura.
- Se dividirá 360 entre la cantidad de lados que tendrá nuestro polígono regular.
- El resultado de esta división será la medida del ángulo central de acuerdo a la cantidad se realizarán las marcas que serán los vértices en nuestra figura.
- Las marcas se unirán cuidando que cada una esté a la misma distancia desde el centro de la figura para que resulte un polígono regular.
Observa las imagenes.
Tema. Cálculo de la medida de los ángulos externos de un polígono.
Como el nombre lo indica los ángulos externos de un polígono son los que se forman fuera de su perímetro.
Para hacer el cálculo correcto se debe extender la línea recta de una de las aristas, esto servirá para medir los grados el ángulo externo.
Recuerda que siempre el ángulo exterior sumado con el ángulo interior sumarán 180 grados.
Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.
Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.
Ejemplos.
Tema. Cálculo de la medida de los ángulos internos de un polígono.
Como el nombre lo indica los ángulos internos de un polígono son los que se forman dentro de su perímetro.
Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.
En caso de que el ángulo sea mayor de 180° simplemente se deben sumar los grados que hacen falta hasta donde se separan las aristas.
Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.
Ejemplo.
La regla general para polígonos regulares.
Así que cada vez que añadimos un lado más (de triángulo a cuadrilátero, a pentágono, etc) sumamos otros 180° al total:
| Si es regular... | ||||
| Figura | Lados | Suma de los ángulos interiores | Forma | Cada ángulo |
|---|---|---|---|---|
| Triángulo | 3 | 180° | 60° | |
| Quadrilátero | 4 | 360° | 90° | |
| Pentágono | 5 | 540° | 108° | |
| Hexágono | 6 | 720° | 120° | |
| ... | ... | .. | ... | ... |
| Cualquier polígono | n | (n-2) × 180° | (n-2) × 180° / n | |
La última línea puede ser un poco difícil de entender, así que vamos a ver un ejemplo.
Ejemplo: ¿Qué pasa con un decágono (10 lados)?
 |
Suma de los ángulos interiores = (n-2) × 180° = (10-2)×180° = 8×180° = 1440°
Y, si es regular, cada ángulo interior = 1440°/10 = 144° |
Semejanza
4.3 semejanza de triangulos
Tema. Semejanza en figuras.
La semejanza en figuras se refiere a 2 imágenes que tienen forma similar.
Para que se aplique la semejanza los ángulos entre las figuras deben ser los mismos.
Una figura semejante tiene un tamaño proporcional a la figura original, esto significa que las medidas de la figura original se dividen todas entre la misma cantidad o se multiplican todas por la misma cantidad. Los resultados permitirán construir la figura semejante.
Ejemplo.
En el siguiente ejemplo las figuras mantienen los mismos ángulos, pero las medidas se duplicaron en la figura semejante.
Tema. Criterios de semejanza en triángulos.
1. Dos triángulos son semejantes si tienen dos ángulos iguales.
2. Dos triángulos son semejantes si tienen los lados proporcionales.
3. Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.
Cálculo de a.
Los pasos son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de a.
Ejemplo.
Cuál será la medida del lado A en el siguiente caso.
La fórmula que se utiliza en este caso es:
a²=c²-b²
Sustituimos los datos en la fórmula:
a²=5²-4²
Resolvemos respetando la jerarquía de operaciones:
a²=25 - 16
a²=9
En el siguiente paso el cuadrado de la letra b pasa de lado contrario como una raíz cuadrada quedando así:
a=√9
a=3
Actividad. Calcular el lado a, para cada una de las siguientes situaciones , observa las medidas.
Los pasos son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de a.
Ejemplo.
Cuál será la medida del lado A en el siguiente caso.
La fórmula que se utiliza en este caso es:
a²=c²-b²
Sustituimos los datos en la fórmula:
a²=5²-4²
Resolvemos respetando la jerarquía de operaciones:
a²=25 - 16
a²=9
En el siguiente paso el cuadrado de la letra b pasa de lado contrario como una raíz cuadrada quedando así:
a=√9
a=3
Actividad. Calcular el lado a, para cada una de las siguientes situaciones , observa las medidas.
4.5 razones trigonometricas
Tema. Funciones trigonométricas.
Para utilizar las funciones trigonometricas debemos identificar los catetos y la hipotenusa en un triángulo rectángulo, ten en cuenta que sólo aplica para este tipo de triángulo.
- La hipotenusa (h)
- El cateto opuesto (depende de qué angulo se busca)
- El cateto adyacente (depende de que angulo se busca)
Funciones trigonometricas.
sen=seno
cos=coseno
tan=tangente
csc=cosecante
sec=secante
cot=cotangente
Ejemplo. Observa el siguiente triángulo, las medidas se han sustituido en cada una de las funciones trigonometricas dependiendo del ángulo solicitado.
Tema. Cálculo de la medida de ángulo Alfa.
Para calcular la medida del ángulo alfa utilizando seno, coseno y tangente, se debe:
Para calcular el ángulo alfa a partir de seno se debe realizar lo siguiente:
1. Presiona la tecla shift, después la tecla sin, en seguida anota la fracción correspondiente a seno.
En tu calculadora debe estar así.
Al presionar la tecla igual tu resultado será:
ahora presiona la tecla
Para calcular este mismo ángulo pero con la función coseno y tangente se realiza el mismo proceso sólo se debe seleccionar la tecla cos o la tecla tan dependiendo de la función que se utiliza.
Para calcular el ángulo beta sólo se debe restar la medida del ángulo alfa al 90°.
Ahora calcula el ángulo alfa para los siguientes triángulos.
Obtén el ángulo Alfa y Beta de los siguientes triángulos, utiliza seno, coseno o tangente.
Tema. Cómo calcular un cateto a partir de un ángulo.
Se puede calcular la longitud de un cateto (opuesto o adyacente) o la hipotenusa, cuándo se sabe la medida de un ángulo y un lado.
Ejemplo.
Calcula la medida del lado desconocido a partir de los datos indicados, observa la imagen.
En este caso el lado x corresponde al cateto opuesto, el lado que mide 11 metros corresponde a la hipotenusa, teniendo estos datos la función que sirve es seno.
2. Se ordenan los datos y se realizan los despejes correspondientes.
El objetivo es dejar sola la letra x, en este caso se se mueve el número 11 del otro lado del signo igual y ahora multiplicará a seno de 42 grados. en la calculadora se debe notar el número 11 por seno de 42.
Ejemplo.
Cuál sería la medida del valor desconocido de acuerdo a los datos indicados.
1. Identificar lados.
en este caso la letra x corresponde al cateto adyacente y el número 11 a la medida de la hipotenusa, por lo tanto la función que sirve que es coseno.
2. Ordenar datos y realizar los despejes.
El número 11 se mueve del otro lado del signo igual y quedará multiplicando a coseno de 42.
Ejemplo.
Calcula la medida del lado indicado.
1. Identificar los lados.
2. Ordenar datos y realizar despejes.
Para todas las situaciones se debe realizar el mismo procedimiento es importante identificar cada uno de los lados, a partir de ello se utiliza la función correspondiente y se realizan los despejes.
Actividad. Observa los siguientes esquemas y calcula los elementos indicados con la letra x.
1. Cuál es la altura del pino.
2. Cuál es la longitud de la escalera.
3. Cuál es el ángulo que se forma entre el poste y el cable que lo sujeta al suelo.
1. Cuál es la altura del pino.
2. Cuál es la longitud de la escalera.
3. Cuál es el ángulo que se forma entre el poste y el cable que lo sujeta al suelo.
Un buzo necesito saber cuántos metros debe caminar para llegar a un barco hundido.
Cuerpos geometricos
4.6 calclulo de perimetros
Tema. Cálculo del perímetro.
El perímetro es la suma de todas las medidas de los lados de una figura.
Para obtenerlo se suman todos los lados sin olvidar colocar la magnitud indicada (es decir, si son cm, m, km,etc.)
Ejemplo.
Cuál es el perímetro de las siguientes figuras.
10+10+10+10+3+7+4+5= 59 cm
6+5+6+5= 22cm
Tema. Longitud de la circunferencia.
Para calcular la medida de la circunferencia se debe multiplicar el diámetro por el valor de pi (3.14).
L=π×d
Ejemplo.
Cuál es la longitud de una circunferencia cuyo diámetro es 10 cm.
L=π x d
L=3.14 x 10cm
L=31.4cm
Actividad. Calcula la longitud de la circunferencia si los diámetros son:
13cm, 11cm, 23cm, 7cm, 8cm,
4.7 calculo de area
Tema. Áreas.
El área es la medida de una superficie en unidades cuadradas (mm², cm², m², km², etc.).
El resultado al calcular una área se puede interpretar como la cantidad de cuadros que caben en la superficie de una figura.
Ejemplo 1.
Si tengo un rectángulo que mide 5cm de base por 2cm de altura. Su área es 10 cm².
Eso significa que dentro de ese rectángulo caben 10 cuadrados que miden un centímetro de cada lado.
Ejemplo 2.
En este ejemplo ocurre lo mismo el cuadrado tiene 4 centímetros de lado, por lo tanto su área será 16cm ²
Ejemplo 3.
En este último ejemplo podemos observar que el área es de un centímetro cuadrado (la de color rojo), sin embargo, podemos marcar el área en milímetros (de color azul).
Para calcular el área se debe conocer la fórmula de cada figura.
Área de un triángulo
Área de un cuadrado
Área de un rectángulo
Área de un rombo
Área del romboide
Área del trapecio
Área de un polígono regular
Área de un polígono
Área de un círculo
Tema. Área del segmento del círculo.
Para calcular el área de un círculo se utiliza la fórmula π x r², pero qué pasaría si sólo me piden un segmento del área de un círculo, tendría que utilizar la fórmula:
Ejemplo: Cuál es el área del siguiente segmento de círculo.
4.8 caculo de volumenes
Para calcular el volumen de cualquier prisma se debe obtener el área y multiplicarlo por su altura.
Un prisma rectangular (u ortoedro) es un poliedro cuya superficie está formada por dosrectángulos iguales y paralelos llamados bases y por cuatro caras laterales que son tambiénrectángulos paralelos e iguales dos a dos.
Su volumen se calcula como el producto de sus dimensiones (las aristas a, b y h).

El volumen del prisma es el producto del área de la base (Ab) por la altura (h). En este caso, la base es un rectángulo, por lo que su área es el producto de los dos lados contiguos (a·b).
Ejemplo

Sea un prisma rectangular de dimensiones conocidas, siendo los costados contiguos de la base a=3 cm y b=1,5 cm y la altura h=4 cm.
¿Cuál es su volumen?
Aplicando la fórmula anterior obtenemos:

Tema. Volumen de cilindro.
La fórmula que se utiliza para obtener el volumen de cilindro es:
V=π • r² • h
El valor de π (pi) es 3.14
La letra r se refiere al radio de la base del cilindro.
La letra h se refiere a la altura del cilindro.
Observa el ejemplo.
Recuerda que el resultado siempre tendrá unidades cúbicas porque se está usando volumen, es decir, mm³, cm³, m³, etcétera.
Tema. Volumen del cono.
Para resolverlo se utiliza la fórmula anterior es el mismo procedimiento que en el cilindro sólo que al final el resultado se divide entre 3.
El valor de π (pi) es 3.14
La letra r se refiere al radio de la base del cono.La letra h se refiere a la altura del cono.



















































.jpg)

























.jpg)
.jpg)
















































